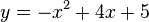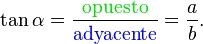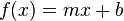Blog

Historia De Las Funciones

19.05.2011 20:41

Mientras que el cálculo diferencial e integral surgió en el siglo XVII, el concepto de función vino a conocerse un siglo despúes, y el limite, entendido de una manera formal y rigurosa, solo a finales del siglo XIX, lo cual difiere de la forma como se presenta actualmente el cálculo, en donde primero se enseñan funciones, luego limites y finalmente derivadas o integrales. En la obra Introductio in Analysi Infinitorum, Leonhard Euler intenta por primera vez dar una definición formal del concepto de función al afirmar que: ``Una función de cantidad variable es una expresión analítica formada de cualquier manera por esa cantidad variable y por numeros o cantidades constantes''. como puede observarse, esta definición difiere de la que actualmenet se conoce, pues siete años despúes, en el prólogo de las Instituciones, calculo diferencial, afirmó:''Algunas cantidades en verdad dependen de otras, si al ser combinadas las ultimas las primeras también sufren cambio, y entonces las primeras se llaman funciones de las últimas. esta denominación es bastante natural y comprende cada metodo mediante el cual una cantidad puede ser determinada por otras. asi, si x denota una cantidad variable, entonces todas las cantidades que dependen de x en cualquier forma estan determinadas por x y se les llama funciones de x''.

 

En la historia de las matemáticas se le dan creditos al matemático suizo Leonhard Euler(1707-1783) por precisar el concepto de función, asi como por realizar un estudio sistemático de todas las funciones elementales, incluyendo sus derivadas e integrales; sin embargo, el concepto mismo de función nació con las primeras relaciones observadas entre dos variables, hecho que seguramente surgió desde los inicios de la matemática en la humanidad, con civilizaciones como la babilonica, la egipcia y la china.

Antes de Euler, el matemático y filosofo francés Rene Descartes(1596-1650) mostró en sus trabajos de geometria que tenía una idea muy clara de los conceptos de ``variable'' y ``función'', realizando una clasificación de las curvas algebraicas según sus grados, reconociendo que los puntos de intersección de dos curvas se obtienen resolviendo, en forma simultanea, las ecuaciones que las representan.

Funciones: Sabias que?

15.05.2011 22:05

 

 La terminología asociada a las funciones se debe al matemático alemán Johann Peter Gustav Lejeune Dirichlet(1805-1859), quien escribió: “Una variable es un símbolo que representa un número dentro de un conjunto de ellos; si dos variables X e y están asociadas de tal forma que al asignar un valor a x  entonces, por alguna regla o correspondencia, se asigna automáticamente un valor a y, se dice que es una función (Univoca) de x. La variable x, a la que se asignan libremente valores, se llama variable independiente, mientras que la variable y, cuyos valores dependen de x, se llama variable dependiente. Los valores permitidos de x constituyen el dominio de definición de la función y los valores de y constituyen su recorrido.”

C:FakepathFunciones
View more presentations from velasquezana4

 

Aplicaciones De Las FunciOnes.

 

  Se puede considerar una Función como una asociación entre dos conjuntos de acuerdo con cierta regla, un proceso llamado aplicación. Dados dos conjuntos S1, y S2, una aplicación de S1 en S2 es una operación que a todo miembro m de S1le asocia un único miembro n de S2. Una función definida en el conjunto de los números reales R y con valores en R es una aplicación, ya que asocia un valor de R, llamado x, a otro valor de R, llamado f(x).

 

      Los conceptos y definiciones de las funciones pueden expresarse en términos de aplicaciones. Una aplicación siempre da un único valor f(x) para cada x, pero no es necesario que un f(x) procede de un solo x, se dice que la función es inyectiva. Un mapa geográfico es un ejemplo de aplicación matemática, ya que aplica puntos de la superficie de la tierra a puntos de una hoja de papel.

  

      Si f aplica un conjunto M en otro N y S es un subconjunto de M, el subconjunto T de N formado aplicando todos los elementos de S se llama imagen de S bajo f y se representa por f(S). El conjunto S formado por todos los elementos de M se aplican en T es llamada imagen inversa o anti imagen, de T y se representa por f-1(T). Si f no es inyectiva, f-1 no es una aplicación, ya que por definición de toda aplicación la imagen es única. En cambio, si f es una aplicación inyectiva, f-1 también lo es. Así f-1 es la llamada aplicación inversa de f, que aplica f(M) en M.

      Si cada miembro de N tiene una anti imagen por f, se dice que f es una aplicación exhaustiva. Si f es inyectiva y exhaustiva (esto es, cuando f-1 es una aplicación y la imagen inversa es única) se dice que la aplicación es biyectiva o biunívoca.

Funciones

 

 

 

Si dos variables X y Y están relacionadas de tal modo que el valor de Y está determinado por el de X, se dice que Y es función de X. en una función a X se le llama variable independiente y a Y variable dependiente, ya que el valor de Y depende de X. el concepto de función fue ya utilizado por un cierto número de matemáticos de siglos pasados, sobre todo por el matemático suizo Leonhard Euler (1707-1789). La notación moderna para representar las funciones, como otras muchas notaciones matemáticas, fue introducida por Euler. Siguiendo, como es usual, la notación de este autor, una función de una variable independiente X se representa por f(x). si se requieren otras funciones, suelen utilizarse los símbolos g(x) y h(x). Las funciones polinómica suelen representarse por P(x) y Q(x). El valor de la función para x = a se representa por f(a). El valor de la función para x = 2 se escribe f(2).

   Por ejemplo, la función definida por:


f(x) = x3 + 4x2 – 7x + 11

Tiene los siguientes valores para los cuatro primeros enteros nulos:

f(1)= 1 + 4 – 7 + 11 = 9
f(2)= 8 + 16 – 14 + 11 = 21
f(3)= 27 + 36 – 21 + 11 = 53
f(4)= 64 + 64 – 28 + 11 =111

Como puede observarse, una función asocia un conjunto de números a otro conjunto de números.

   Las funciones se utilizan en muchas ramas de la ciencia para describir relaciones entre magnitudes físicas. Por ejemplo, la distancia recorrida por un cuerpo en caída libre es una función del tiempo transcurrido.

    Las funciones para las cuales un valor de x da lugar a un solo valor de y se llaman funciones univocas de x. por ejemplo y = x + 3 es una función univoca de x. si un valor de x da lugar a varios valores de y se dice que y es una función multivoca de x. por ejemplo, y = √x (suponiendo que x e y son números reales) tiene dos valores de x para cada valor de y, por lo que se trata de una función multivoca.

Puede ocurrir que la función solo tenga sentido para determinados valores de x. estos valores permitidos de x constituyen entonces el dominio de la función por ejemplo, la función:

y = √1-x 2,

   Sólo tiene sentido ( para números reales) si x pertenece al intervalo comprendido entre +1 y -1 (incluyendo x = ± 1); de lo contrario, y seria la raíz cuadrada de un número negativo. En consecuencia, el dominio de la función es el intervalo -1 ≤ x ≤ 1. Los correspondientes valores de y constituyen el recorrido de la función. En el caso anterior, el recorrido es 0 ≤ y ≤ 1.

 

Tipos de Funciones 

 

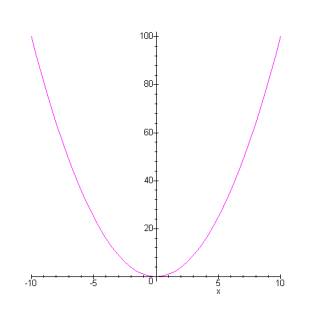
Función cuadrática

En matemáticas una función cuadrática o función de segundo grado es una función polinómica que se define mediante un polinomio de segundo grado como:

 

f(x) = ax^2 + bx + c \,

donde a, b y c son constantes y a es distinto de 0.

La representación gráfica en el plano XY haciendo:

y = f(x) \,

esto es:

 

y = ax^2 + bx + c \,

es una parábola vertical, orientada hacia arriba o hacia abajo según el signo de a.

 

 

 

Estudio de la función


Corte con el eje y

Función cuadrática 03.svg

La función corta el eje y en el punto y = f(0), es decir, la parábola corta el eje y cuando x vale cero (0):

y = f(0) = a \cdot 0^2 + b \cdot 0 + c \,

lo que resulta:

y = f(0) = c \,

la función corta el eje y en el punto (0, c), siendo c el termino independiente de la función.


Corte con el eje x

La función corta al eje x cuando y vale 0, dada la función:

y = ax^2 + bx + c \,

tendremos que:

y = 0 \quad \longmapsto \quad ax^2 + bx + c = 0 \,

las distintas soluciones de esta ecuación de segundo grado, son los casos de corte con el eje x, que se obtienen como es sabido por la expresión:

x = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a}

donde:

b^2 - 4 a c \,

se le llama discriminante, Δ:

\Delta = b^2 - 4 a c \,

según el signo del discriminante podemos distinguir:


Discriminante positivo

Función cuadrática 11.svg
Δ > 0, la ecuación tiene dos soluciones, y por tanto la parábola cortara al eje x en dos puntos: x1 y x2.

Veamos por ejemplo la función:

y = -x^2 + 4x + 5 \,

que cortara el eje x cuando:

y = 0 \quad \longmapsto \quad -x^2 + 4x + 5 = 0 \,

que tendrá por solución general:

x = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a}

en este caso:

x = \frac{-4 \pm \sqrt{4^2 - 4 (-1) 5}}{2 (-1)}

que resulta:

x = \frac{-4 \pm \sqrt{16 + 20}}{-2}

Para esta ecuación el discriminante tiene valor positivo:

\Delta = 16 + 20 = 36 \,

y por tanto tiene dos soluciones:

x_1 = \frac{-4 + \sqrt{36}}{-2} \quad x_2 = \frac{-4 - \sqrt{36}}{-2}

operando:

x_1 = \frac{-4 + 6}{-2} \quad x_2 = \frac{-4 - 6}{-2}
x_1 = \frac{2}{-2} \quad x_2 = \frac{-10}{-2}
x_1 = -1 \quad x_2 = 5

Los puntos: (-1,0), (5,0) son los de corte con el eje x, como se puede ver en la figura.

 

Función trigonométrica

 

Las funciones trigonométricas, en matemáticas, son relaciones angulares que se utilizan para relacionar los ángulos del triángulo con las longitudes de los lados del mismo según los principios de la Trigonometría.

Las funciones trigonométricas son de gran importancia en física, astronomía, cartografía, náutica, telecomunicaciones, la representación de fenómenos periódicos, y otras muchas aplicaciones.

 

 Archivo:Circle-trig6.svg

Definiciones respecto de un triángulo rectángulo

Trigono a10.svg

Para definir las razones trigonométricas del ángulo: α, del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:

  • La hipotenusa (h) es el lado opuesto al ángulo recto, o lado de mayor longitud del triángulo rectángulo.
  • El cateto opuesto (a) es el lado opuesto al ángulo que queremos determinar.
  • El cateto adyacente (b) es el lado adyacente al ángulo del que queremos determinar.

Todos los triángulos considerados se encuentran en el Plano Euclidiano, por lo que la suma de sus ángulos internos es igual a π radianes (o 180°). En consecuencia, en cualquier triángulo rectángulo los ángulos no rectos se encuentran entre 0 y π/2 radianes. Las definiciones que se dan a continuación definen estrictamente las funciones trigonométricas para ángulos dentro de ese rango:

1) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa:

\sin \alpha = \frac {{ \color{ForestGreen}\textrm{opuesto}}} {{ \color{Red}\textrm{hipotenusa}}} = \frac {a} {h}.

El valor de esta relación no depende del tamaño del triángulo rectángulo que elijamos, siempre que tenga el mismo ángulo α , en cuyo caso se trata de triángulos semejantes.

2) El coseno de un ángulo es la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa:

\cos \alpha = \frac {{ \color{Blue}\textrm{adyacente}}} {{ \color{Red}\textrm{hipotenusa}}} = \frac {b} {h}.

3) La tangente de un ángulo es la relación entre la longitud del cateto opuesto y la del adyacente:

\tan \alpha = \frac {{ \color{ForestGreen}\textrm{opuesto}}} {{ \color{Blue}\textrm{adyacente}}} = \frac {a} {b}.

4) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto:

\cot \alpha = \frac {{ \color{Blue}\textrm{adyacente}}} {{ \color{ForestGreen}\textrm{opuesto}}} = \frac {b} {a}.

5) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente:

\sec \alpha = \frac {{ \color{Red}\textrm{hipotenusa}}} {{ \color{Blue}\textrm{adyacente}}} = \frac {h} {b}.

6) La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto:

\csc \alpha = \frac {{ \color{Red}\textrm{hipotenusa}}} {{ \color{ForestGreen}\textrm{opuesto}}} = \frac {h} {a}.

 

Función polinómica

 

En matemática, las funciones polinómicas son las funciones

f:x \mapsto P(x)\,
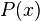donde P(x)\, es un polinomio en 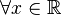x\,, \forall x\in\mathbb{R}, es decir, una suma finita de potencias de x\, multiplicados por coeficientes reales, de la forma:
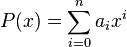
P(x)=\sum_{i=0}^n a_i x^i

Funciones polinómicas básicas

Algunas funciones polinómicas reciben un nombre especial según el grado del polinomio:

Grado Nombre Expresión
0 función constante y = a
1 función lineal y = ax + b es un binomio del primer grado
2 función cuadrática y = ax² + bx + c es un trinomio del segundo grado
3 función cúbica y = ax³ + bx² + cx + d es un cuatrinomio de tercer grado
 

 

 

 

 

Función lineal

 

En matemática, el término función lineal puede referirse a dos conceptos diferentes.

En el primero, correspondiente a la geometría y el álgebra elemental, una función lineal es una función polinómica de primer grado. Es decir, una función que se representa en el plano cartesianocomo una línea recta.

Esta función se puede escribir como

f(x) = m x + b \,

donde m y b son constantes reales y x es una variable real. La constante m es la pendiente de la recta, y b es el punto de corte de la recta con el eje y. Cuando cambiamos m modificamos la inclinación de la recta y cuando cambiamos b desplazamos la línea arriba o abajo.

En el segundo caso, en matemáticas más avanzadas, una función lineal es una función que es una aplicación lineal. Esto es, una aplicación entre dos espacios vectoriales que preserva la suma de vectores y la multiplicación por un escalar.

Una función lineal según la primera definición dada anteriormente representa una aplicación lineal si y sólo si b = 0. Así, algunos autores llaman función lineal a aquella de la forma f(x) = mx mientras que llaman función afín a la que tiene la forma f(x) = mx + b cuando b es distinto de cero..

 

 

Ejemplo

FuncionLineal03.svg

Una función lineal de una única variable dependiente x suele escribirse en la forma siguiente